This function applies the probability integral transformation (PIT) for R-vine copula models to given copula data.
RVinePIT(data, RVM)Arguments
- data
An N x d data matrix (with uniform margins).
- RVM
RVineMatrix()objects of the R-vine model.
Value
An N x d matrix of PIT data from the given R-vine copula
model.
Details
The multivariate probability integral transformation (PIT) of Rosenblatt
(1952) transforms the copula data \(u = (u_1,\ldots,u_d)\) with a given
multivariate copula C into independent data in \([0,1]^d\), where d is the
dimension of the data set.
Let \(u = (u_1,\ldots,u_d)\) denote copula data of dimension d. Further let C be the joint cdf of \(u = (u_1,\ldots,u_d)\). Then Rosenblatt's transformation of u, denoted as \(y = (y_1,\ldots,y_d)\), is defined as $$ y_1 := u_1,\ \ y_2 := C(u_2|u_1), \ldots\ y_d := C(u_d|u_1,\ldots,u_{d-1}), $$ where \(C(u_k|u_1,\ldots,u_{k-1})\) is the conditional copula of \(U_k\) given \(U_1 = u_1,\ldots, U_{k-1} = u_{k-1}, k = 2,\ldots,d\). The data vector \(y = (y_1,\ldots,y_d)\) is now i.i.d. with \(y_i \sim U[0, 1]\). The algorithm for the R-vine PIT is given in the appendix of Schepsmeier (2015).
References
Rosenblatt, M. (1952). Remarks on a Multivariate Transformation. The Annals of Mathematical Statistics 23 (3), 470-472.
Schepsmeier, U. (2015) Efficient information based goodness-of-fit tests for vine copula models with fixed margins. Journal of Multivariate Analysis 138, 34-52.
See also
Examples
# load data set
data(daxreturns)
# select the R-vine structure, families and parameters
RVM <- RVineStructureSelect(daxreturns[,1:3], c(1:6))
# PIT data
pit <- RVinePIT(daxreturns[,1:3], RVM)
par(mfrow = c(1,2))
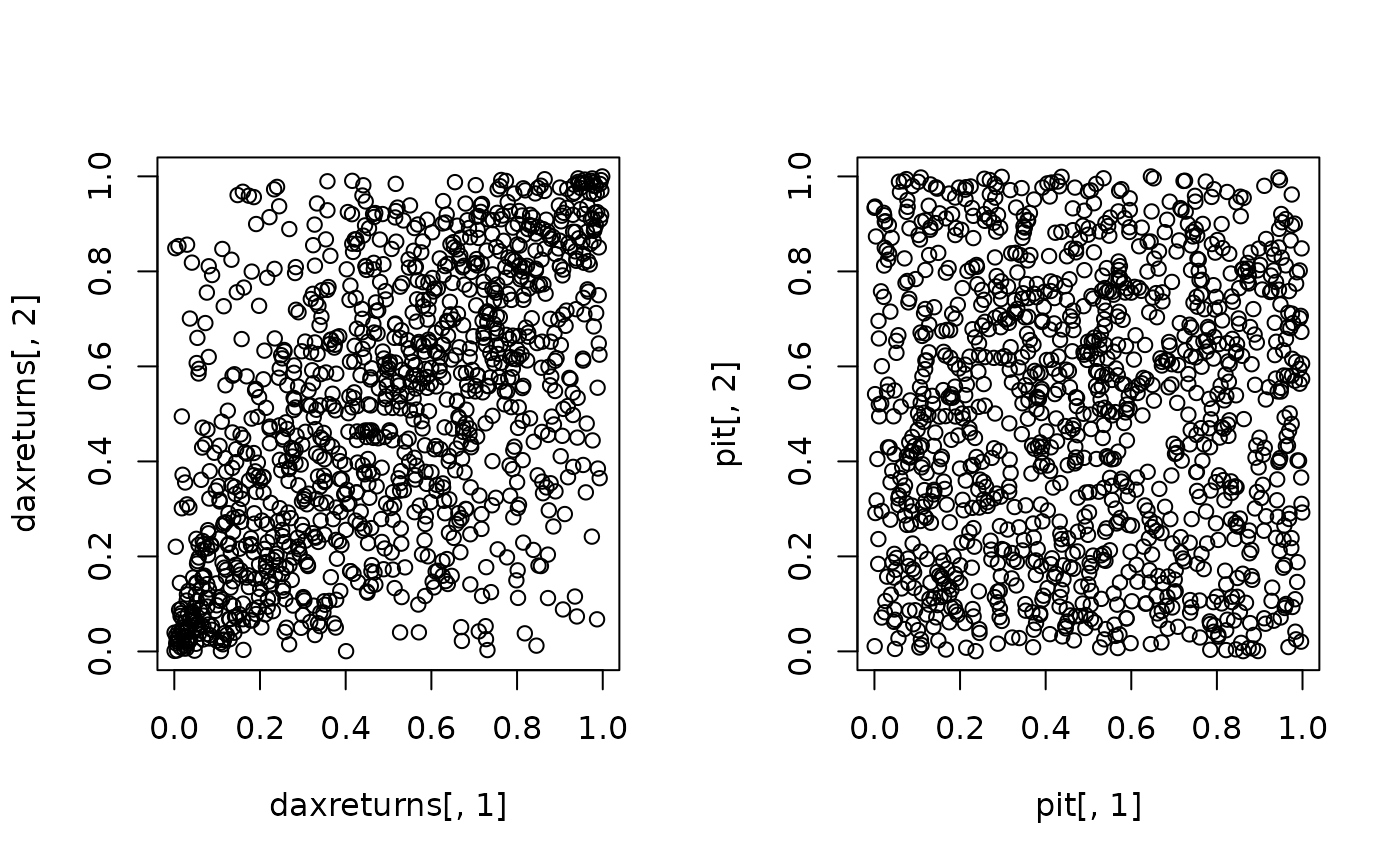
plot(daxreturns[,1], daxreturns[,2]) # correlated data
plot(pit[,1], pit[,2]) # i.i.d. data
cor(pit, method = "kendall")
#> [,1] [,2] [,3]
#> [1,] 1.000000000 0.010307462 0.002118217
#> [2,] 0.010307462 1.000000000 -0.002751145
#> [3,] 0.002118217 -0.002751145 1.000000000