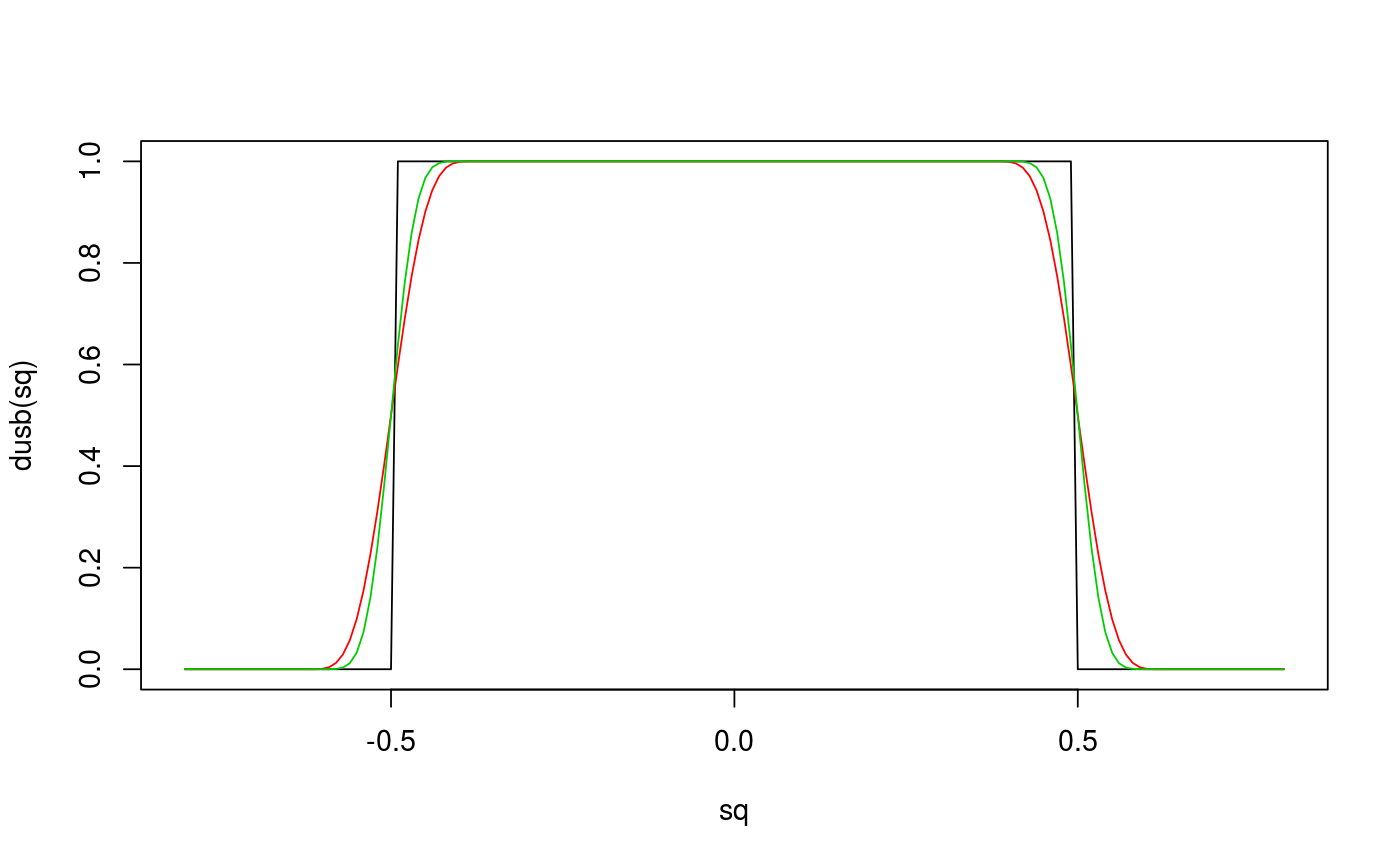
Uniform scaled beta distribution

The uniform scaled beta (USB) distribution describes the distribution of the random variable $$U_{b, \nu} = U + \theta(B - 0.5),$$ where \(U\) is a \(U[-0.5, 0.5]\) random variable, \(B\) is a \(Beta(\nu, \nu)\) random variable, and \(theta > 0, \nu >= 1\).

dusb(x, theta = 0, nu = 5)

rusb(n, theta = 0, nu = 5, quasi = FALSE)

Arguments

x	vector of quantiles.
theta	scale parameter of the USB distribution.
nu	smoothness parameter of the USB distribution.
n	number of observations.
quasi	logical indicating whether quasi random numbers (qrng::ghalton()) should be used for generating uniforms (which are then transformed by the quantile function)

References

Nagler, T. (2017). A generic approach to nonparametric function estimation with mixed data. arXiv:1704.07457

Examples

# plot distribution
sq <- seq(-0.8, 0.8, by = 0.01)
plot(sq, dusb(sq), type = "l")
lines(sq, dusb(sq, theta = 0.25), col = 2)
lines(sq, dusb(sq, theta = 0.25, nu = 10), col = 3)

# simulate from the distribution
x <- rusb(100, theta = 0.3, nu = 0)