Note: This function is deprecated and only available for backwards
compatibility. See contour.BiCop() for contour plots of
parametric copulas, and BiCopKDE() for kernel estimates.
BiCopMetaContour(
u1 = NULL,
u2 = NULL,
bw = 1,
size = 100,
levels = c(0.01, 0.05, 0.1, 0.15, 0.2),
family = "emp",
par = 0,
par2 = 0,
PLOT = TRUE,
margins = "norm",
margins.par = 0,
xylim = NA,
obj = NULL,
...
)Arguments
- u1, u2
Data vectors of equal length with values in \([0,1]\) (default:
u1andu2 = NULL).- bw
Bandwidth (smoothing factor; default:
bw = 1).- size
Number of grid points; default:
size = 100.- levels
Vector of contour levels. For Gaussian, Student-t or exponential margins the default value (
levels = c(0.01, 0.05, 0.1, 0.15, 0.2)) typically is a good choice. For uniform margins we recommendlevels = c(0.1, 0.3, 0.5, 0.7, 0.9, 1.1, 1.3, 1.5)
and for Gamma marginslevels = c(0.005, 0.01, 0.03, 0.05, 0.07, 0.09).- family
An integer defining the bivariate copula family or indicating an empirical contour plot:
"emp"= empirical contour plot (default; margins can be specified bymargins)0= independence copula1= Gaussian copula2= Student t copula (t-copula)3= Clayton copula4= Gumbel copula5= Frank copula6= Joe copula7= BB1 copula8= BB6 copula9= BB7 copula10= BB8 copula13= rotated Clayton copula (180 degrees;survival Clayton'') \cr `14` = rotated Gumbel copula (180 degrees;survival Gumbel”)16= rotated Joe copula (180 degrees;survival Joe'') \cr `17` = rotated BB1 copula (180 degrees;survival BB1”)18= rotated BB6 copula (180 degrees;survival BB6'')\cr `19` = rotated BB7 copula (180 degrees;survival BB7”)20= rotated BB8 copula (180 degrees; “survival BB8”)23= rotated Clayton copula (90 degrees)
`24` = rotated Gumbel copula (90 degrees)
`26` = rotated Joe copula (90 degrees)
`27` = rotated BB1 copula (90 degrees)
`28` = rotated BB6 copula (90 degrees)
`29` = rotated BB7 copula (90 degrees)
`30` = rotated BB8 copula (90 degrees)
`33` = rotated Clayton copula (270 degrees)
`34` = rotated Gumbel copula (270 degrees)
`36` = rotated Joe copula (270 degrees)
`37` = rotated BB1 copula (270 degrees)
`38` = rotated BB6 copula (270 degrees)
`39` = rotated BB7 copula (270 degrees)
`40` = rotated BB8 copula (270 degrees)
`104` = Tawn type 1 copula
`114` = rotated Tawn type 1 copula (180 degrees)
`124` = rotated Tawn type 1 copula (90 degrees)
`134` = rotated Tawn type 1 copula (270 degrees)
`204` = Tawn type 2 copula
`214` = rotated Tawn type 2 copula (180 degrees)
`224` = rotated Tawn type 2 copula (90 degrees)
`234` = rotated Tawn type 2 copula (270 degrees)- par
Copula parameter; if empirical contour plot,
par = NULLor0(default).- par2
Second copula parameter for t-, BB1, BB6, BB7, BB8, Tawn type 1 and type 2 copulas (default:
par2 = 0).- PLOT
Logical; whether the results are plotted. If
PLOT = FALSE, the valuesx,yandzare returned (see below; default:PLOT = TRUE).- margins
Character; margins for the bivariate copula contour plot. Possible margins are:
"norm"= standard normal margins (default)"t"= Student t margins with degrees of freedom as specified bymargins.par"gamma"= Gamma margins with shape and scale as specified bymargins.par"exp"= Exponential margins with rate as specified bymargins.par"unif"= uniform margins- margins.par
Parameter(s) of the distribution of the margins if necessary (default:
margins.par = 0), i.e.,- xylim
A 2-dimensional vector of the x- and y-limits. By default (
xylim = NA) standard limits for the selected margins are used.- obj
BiCopobject containing the family and parameter specification.- ...
Additional plot arguments.
Value
- x
A vector of length
sizewith the x-values of the kernel density estimator with Gaussian kernel if the empirical contour plot is chosen and a sequence of values inxylimif the theoretical contour plot is chosen.- y
A vector of length
sizewith the y-values of the kernel density estimator with Gaussian kernel if the empirical contour plot is chosen and a sequence of values inxylimif the theoretical contour plot is chosen.- z
A matrix of dimension
sizewith the values of the density of the meta distribution with chosen margins (seemarginsandmargins.par) evaluated at the grid points given byxandy.
Note
The combination family = 0 (independence copula) and
margins = "unif" (uniform margins) is not possible because all
z-values are equal.
See also
Examples
## meta Clayton distribution with Gaussian margins
cop <- BiCop(family = 1, tau = 0.5)
BiCopMetaContour(obj = cop, main = "Clayton - normal margins")
#> Warning: This function is deprecated. See ?contour.BiCop for contour plots of parametric copulas
#> and ?BiCopKDE for kernel estimates.
 # better:
contour(cop, main = "Clayton - normal margins")
# better:
contour(cop, main = "Clayton - normal margins")
 ## empirical contour plot with standard normal margins
dat <- BiCopSim(1000, cop)
BiCopMetaContour(dat[, 1], dat[, 2], bw = 2, family = "emp",
main = "empirical - normal margins")
#> Warning: This function is deprecated. See ?contour.BiCop for contour plots of parametric copulas
#> and ?BiCopKDE for kernel estimates.
## empirical contour plot with standard normal margins
dat <- BiCopSim(1000, cop)
BiCopMetaContour(dat[, 1], dat[, 2], bw = 2, family = "emp",
main = "empirical - normal margins")
#> Warning: This function is deprecated. See ?contour.BiCop for contour plots of parametric copulas
#> and ?BiCopKDE for kernel estimates.
 # better:
BiCopKDE(dat[, 1], dat[, 2],
main = "empirical - normal margins")
# better:
BiCopKDE(dat[, 1], dat[, 2],
main = "empirical - normal margins")
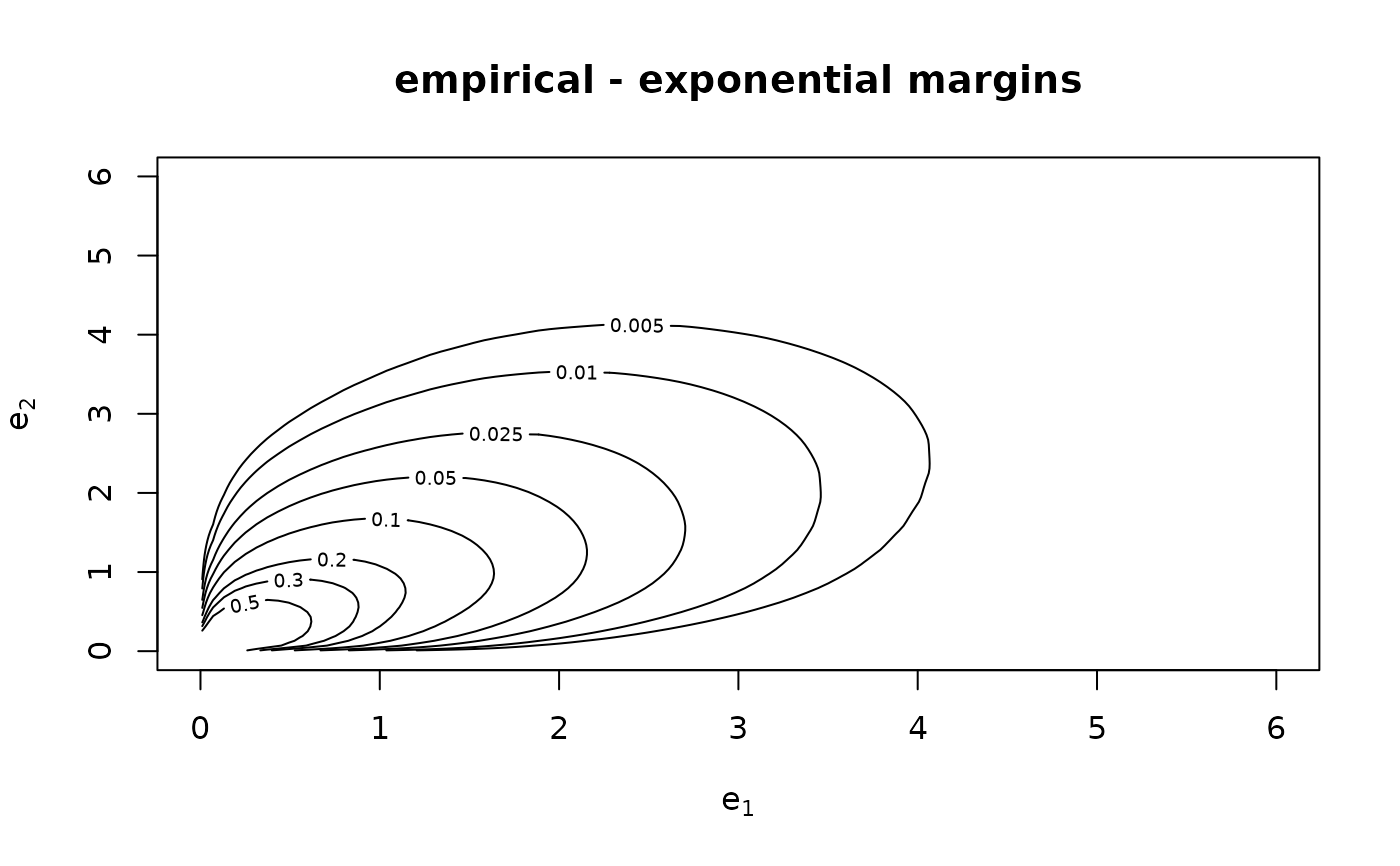
 ## empirical contour plot with exponential margins
BiCopMetaContour(dat[, 1], dat[, 2], bw = 2,
main = "empirical - exponential margins",
margins = "exp", margins.par = 1)
#> Warning: This function is deprecated. See ?contour.BiCop for contour plots of parametric copulas
#> and ?BiCopKDE for kernel estimates.
## empirical contour plot with exponential margins
BiCopMetaContour(dat[, 1], dat[, 2], bw = 2,
main = "empirical - exponential margins",
margins = "exp", margins.par = 1)
#> Warning: This function is deprecated. See ?contour.BiCop for contour plots of parametric copulas
#> and ?BiCopKDE for kernel estimates.
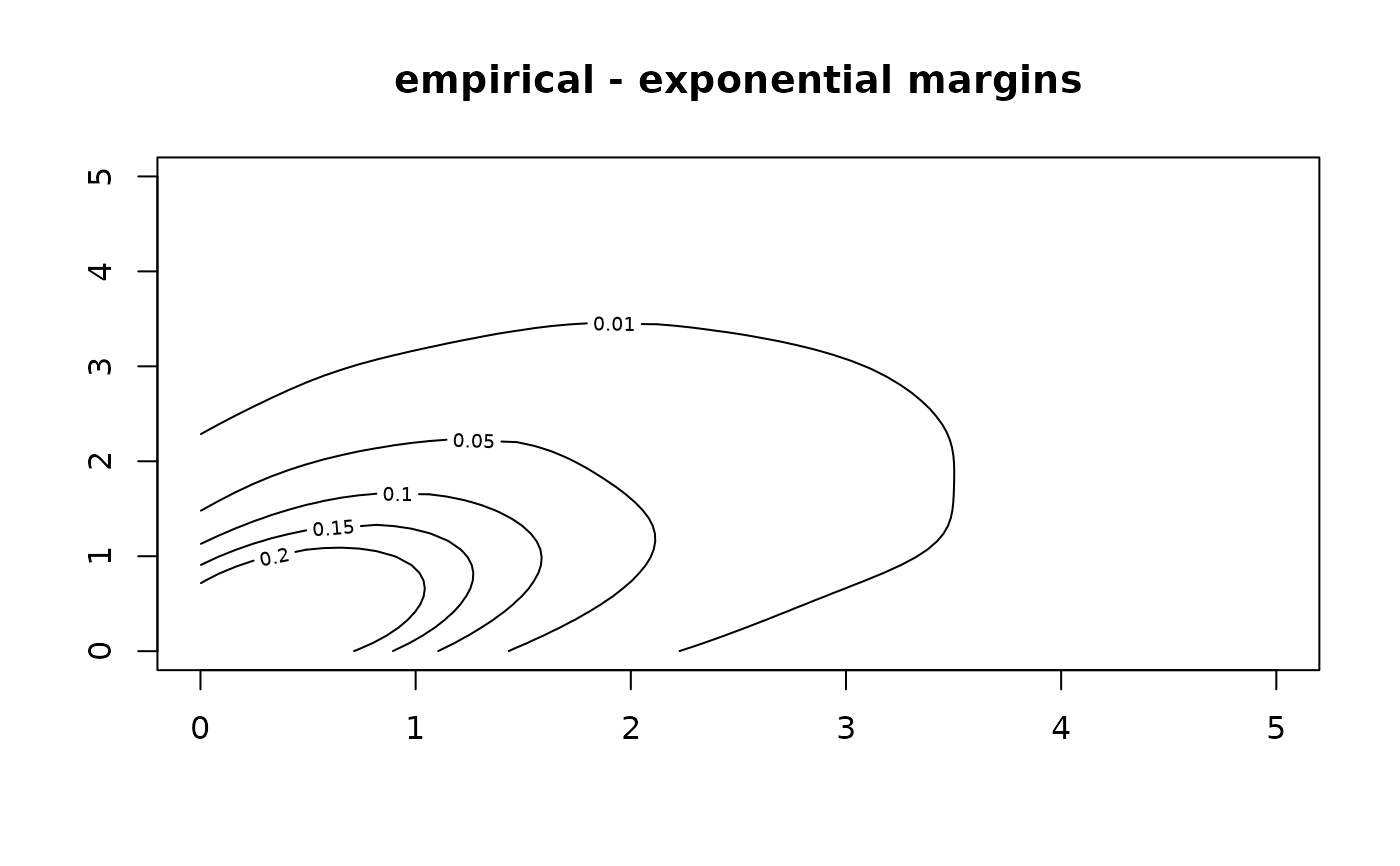 # better:
BiCopKDE(dat[, 1], dat[, 2],
main = "empirical - exponential margins",
margins = "exp")
# better:
BiCopKDE(dat[, 1], dat[, 2],
main = "empirical - exponential margins",
margins = "exp")