Kernel estimation of vine copula densities

Source: R/kdevinecop.R

The function estimates a vine copula density using kernel estimators for the pair copulas (based on the kdecopula package).

kdevinecop(
  data,
  matrix = NA,
  method = "TLL2",
  renorm.iter = 3L,
  mult = 1,
  test.level = NA,
  trunc.level = NA,
  treecrit = "tau",
  cores = 1,
  info = FALSE
)

Arguments

data

(\(n x d\)) matrix of copula data (have to lie in \([0,1^d]\)).

matrix

R-Vine matrix (\(n x d\)) specifying the structure of the vine; if NA (default) the structure selection heuristic of Dissman et al. (2013) is applied.

method

see kdecop.

renorm.iter

see kdecop.

mult

see kdecop.

test.level

significance level for independence test. If you provide a number in \([0, 1]\), an independence test (BiCopIndTest) will be performed for each pair; if the null hypothesis of independence cannot be rejected, the independence copula will be set for this pair. If test.level = NA (default), no independence test will be performed.

trunc.level

integer; the truncation level. All pair copulas in trees above the truncation level will be set to independence.

treecrit

criterion for structure selection; defaults to "tau".

cores

integer; if cores > 1, estimation will be parallized within each tree (using foreach).

info

logical; if TRUE, additional information about the estimate will be gathered (see kdecop).

Value

An object of class kdevinecop. That is, a list containing

T1, T2, ...

lists of the estimted pair copulas in each tree,

matrix

the structure matrix of the vine,

info

additional information about the fit (if info = TRUE).

References

Nagler, T., Czado, C. (2016)
Evading the curse of dimensionality in nonparametric density estimation with simplified vine copulas.
Journal of Multivariate Analysis 151, 69-89 (doi:10.1016/j.jmva.2016.07.003)

Nagler, T., Schellhase, C. and Czado, C. (2017)
Nonparametric estimation of simplified vine copula models: comparison of methods arXiv:1701.00845

Dissmann, J., Brechmann, E. C., Czado, C., and Kurowicka, D. (2013).
Selecting and estimating regular vine copulae and application to financial returns.
Computational Statistics & Data Analysis, 59(0):52--69.

Examples

data(wdbc, package = "kdecopula")
# rank-transform to copula data (margins are uniform)
u <- VineCopula::pobs(wdbc[, 5:7], ties = "average")
u <- u[1:30, ]
fit <- kdevinecop(u)                   # estimate density
dkdevinecop(c(0.1, 0.1, 0.1), fit)     # evaluate density estimate
#> [1] 9.040116e-17
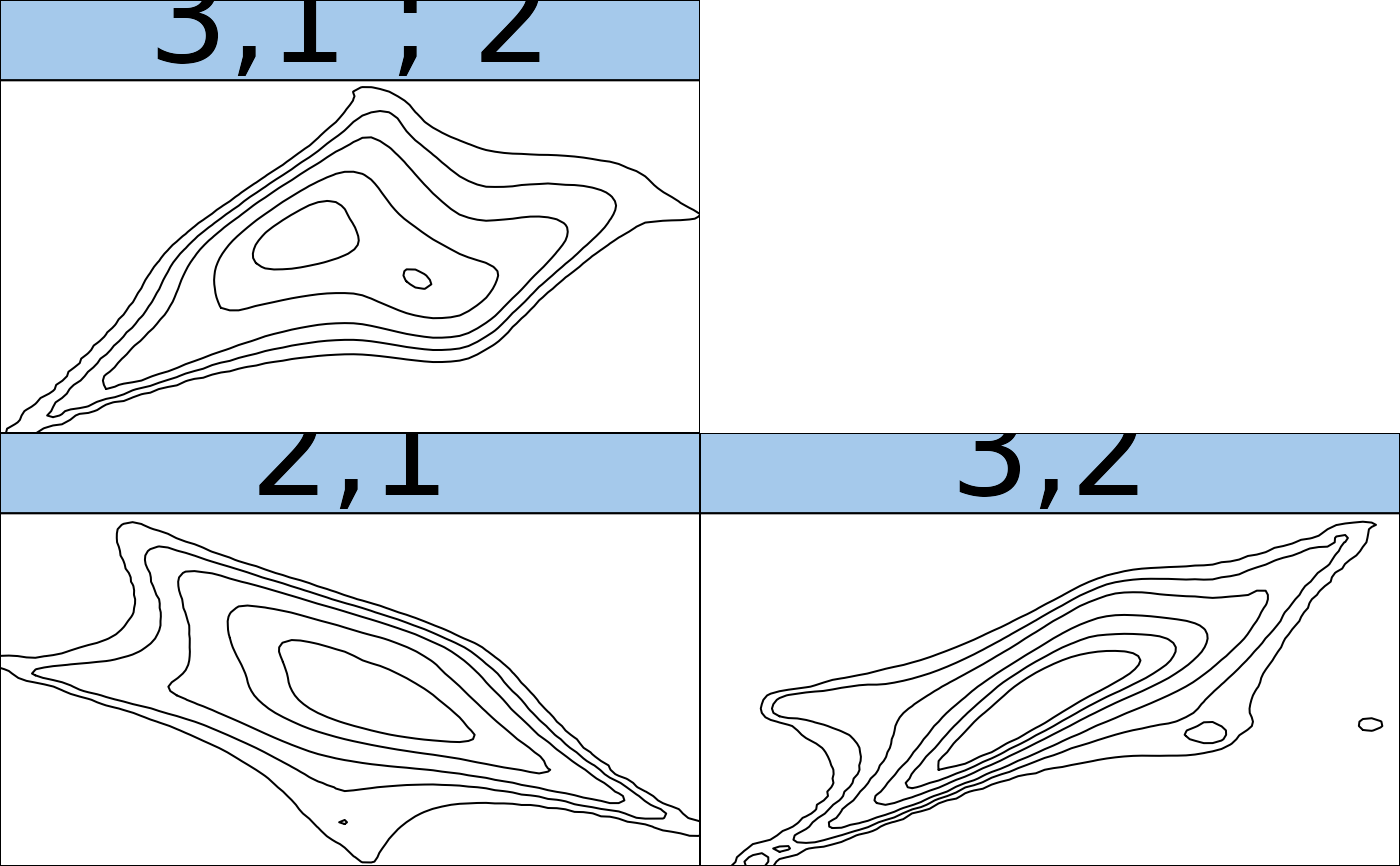
contour(fit)                           # contour matrix (Gaussian scale)

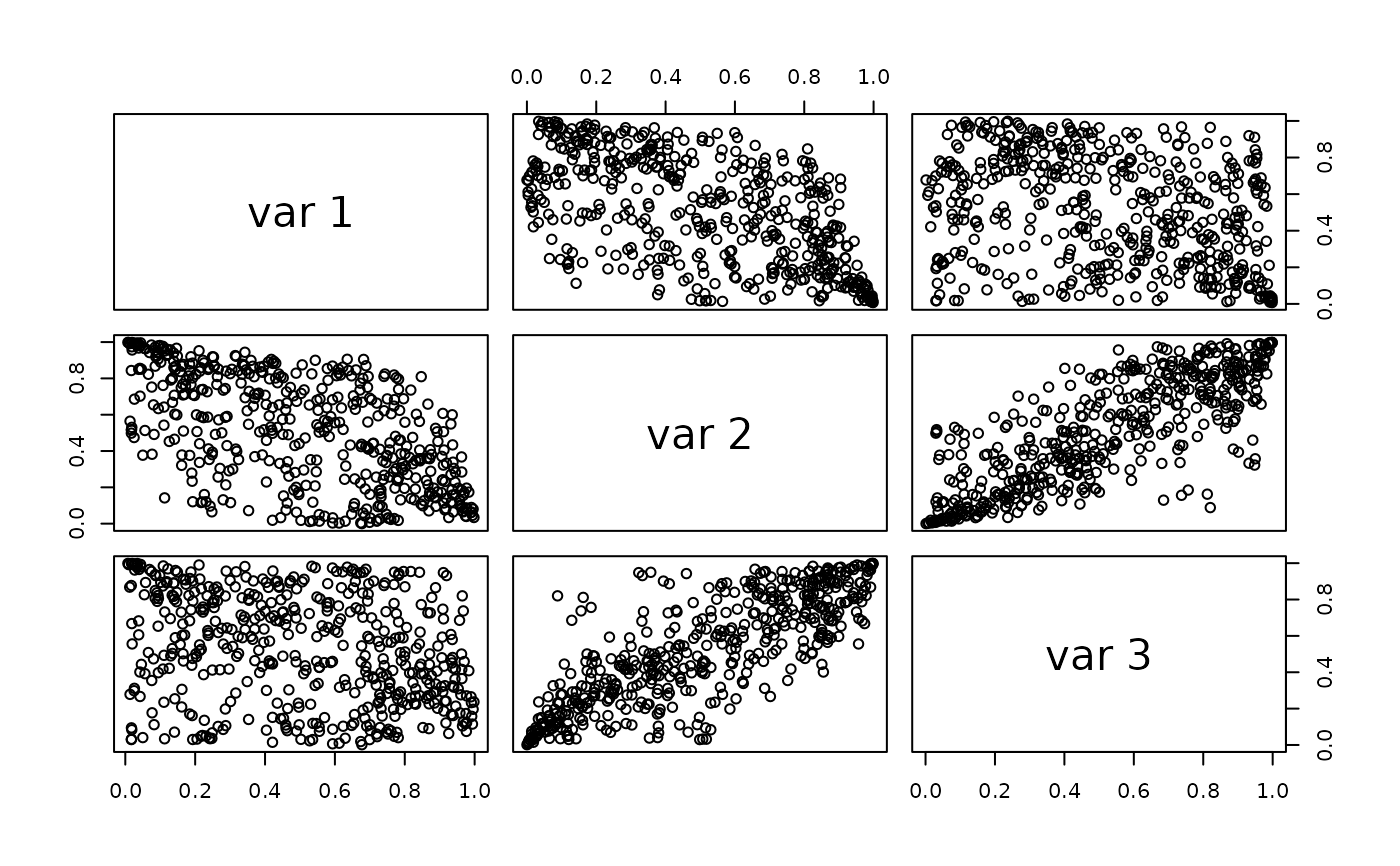
pairs(rkdevinecop(500, fit))           # plot simulated data