Stationary vine copula models

Automated fitting or creation of custom S-vine copula models

svinecop(
  data,
  p,
  var_types = rep("c", NCOL(data)),
  family_set = "all",
  cs_structure = NA,
  out_vertices = NA,
  in_vertices = NA,
  type = "S",
  par_method = "mle",
  nonpar_method = "constant",
  mult = 1,
  selcrit = "aic",
  weights = numeric(),
  psi0 = 0.9,
  presel = TRUE,
  trunc_lvl = Inf,
  tree_crit = "tau",
  threshold = 0,
  keep_data = FALSE,
  show_trace = FALSE,
  cores = 1
)

Arguments

data

a matrix or data.frame (copula data should have approximately uniform margins).

p

the Markov order.

var_types

variable types; discrete variables not (yet) allowed.

family_set

a character vector of families; see rvinecopulib::bicop() for additional options.

cs_structure

the cross-sectional vine structure (see rvinecopulib::rvine_structure(); cs_structure = NA performs automatic structure selection.

out_vertices

the out-vertex; if NA, the out-vertex is selected automatically if no structure is provided, and is equivalent to 1 if a structure is provided.

in_vertices

the in-vertex; if NA, the in-vertex is selected automatically if no structure is provided, and is equivalent to 1 if a structure is provided.

type

type of stationary vine; "S" (default) for general S-vines, "D" for Smith's long D-vine, "M" for Beare and Seo's M-vine.

par_method

the estimation method for parametric models, either "mle" for sequential maximum likelihood, "itau" for inversion of Kendall's tau (only available for one-parameter families and "t".

nonpar_method

the estimation method for nonparametric models, either "constant" for the standard transformation estimator, or "linear"/"quadratic" for the local-likelihood approximations of order one/two.

mult

multiplier for the smoothing parameters of nonparametric families. Values larger than 1 make the estimate more smooth, values less than 1 less smooth.

selcrit

criterion for family selection, either "loglik", "aic", "bic", "mbic". For vinecop() there is the additional option "mbicv".

weights

optional vector of weights for each observation.

psi0

prior probability of a non-independence copula (only used for selcrit = "mbic" and selcrit = "mbicv").

presel

whether the family set should be thinned out according to symmetry characteristics of the data.

trunc_lvl

currently unsupported.

tree_crit

the criterion for tree selection, one of "tau", "rho", "hoeffd", or "mcor" for Kendall's \(\tau\), Spearman's \(\rho\), Hoeffding's \(D\), and maximum correlation, respectively.

threshold

for thresholded vine copulas; NA indicates that the threshold should be selected automatically by rvinecopulib::mBICV().

keep_data

whether the data should be stored (necessary for using fitted()).

show_trace

logical; whether a trace of the fitting progress should be printed.

cores

number of cores to use; if more than 1, estimation of pair copulas within a tree is done in parallel.

Value

Returns the fitted model as an object with classes svinecop and svinecop_dist. Also inherits from vinecop, vinecop_dist

such that many functions from rvinecopulib can be called.

Examples

# load data set
data(returns)  

# convert to pseudo observations with empirical cdf for marginal distributions
u <- pseudo_obs(returns[1:100, 1:3]) 

# fit parametric S-vine copula model with Markov order 1
fit <- svinecop(u, p = 1, family_set = "parametric")
fit 
#> 3-dimensional S-vine copula model of order p = 1 ('svinecop_dist')
summary(fit)
#> # A data.frame: 12 x 10 
#>  tree edge conditioned conditioning var_types   family rotation parameters df
#>     1    1        6, 3                    c,c gaussian        0      -0.24  1
#>     1    2        1, 2                    c,c        t        0 0.72, 2.97  2
#>     1    3        2, 3                    c,c        t        0 0.77, 3.22  2
#>     2    1        5, 3            6       c,c    indep        0             0
#>     2    2        6, 2            3       c,c    indep        0             0
#>     2    3        1, 3            2       c,c    frank        0        1.2  1
#>     3    1        4, 3         6, 5       c,c    indep        0             0
#>     3    2        5, 2         3, 6       c,c      joe        0        1.1  1
#>     3    3        6, 1         2, 3       c,c    indep        0             0
#>     4    1        4, 2      3, 6, 5       c,c    indep        0             0
#>    tau
#>  -0.15
#>   0.51
#>   0.56
#>   0.00
#>   0.00
#>   0.13
#>   0.00
#>   0.04
#>   0.00
#>   0.00
#> # ... with 2 more rows
plot(fit)

contour(fit)

logLik(fit)
#> [1] 87.19237
#> attr(,"df")
#> [1] 8

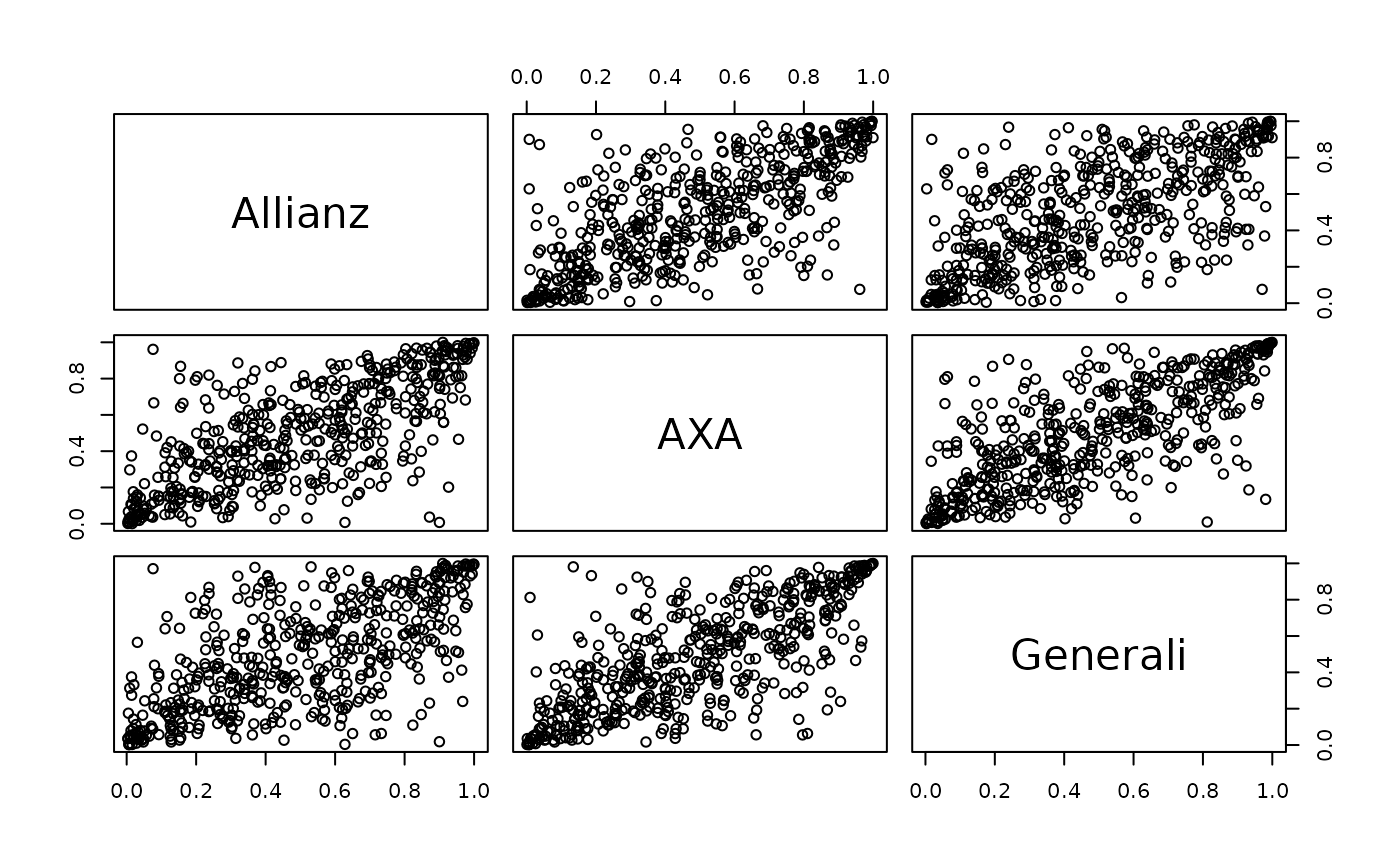
pairs(svinecop_sim(500, rep = 1, fit))