Kendall's Plot for Bivariate Copula Data

This function creates a Kendall's plot (K-plot) of given bivariate copula data.

BiCopKPlot(u1, u2, PLOT = TRUE, ...)

Arguments

u1, u2: Data vectors of equal length with values in $[0,1]$.
PLOT: Logical; whether the results are plotted. If PLOT = FALSE, the values W.in and Hi.sort are returned (see below; default: PLOT = TRUE).
...: Additional plot arguments.

Value

W.in: W-statistics (x-axis).
Hi.sort: H-statistics (y-axis).

Details

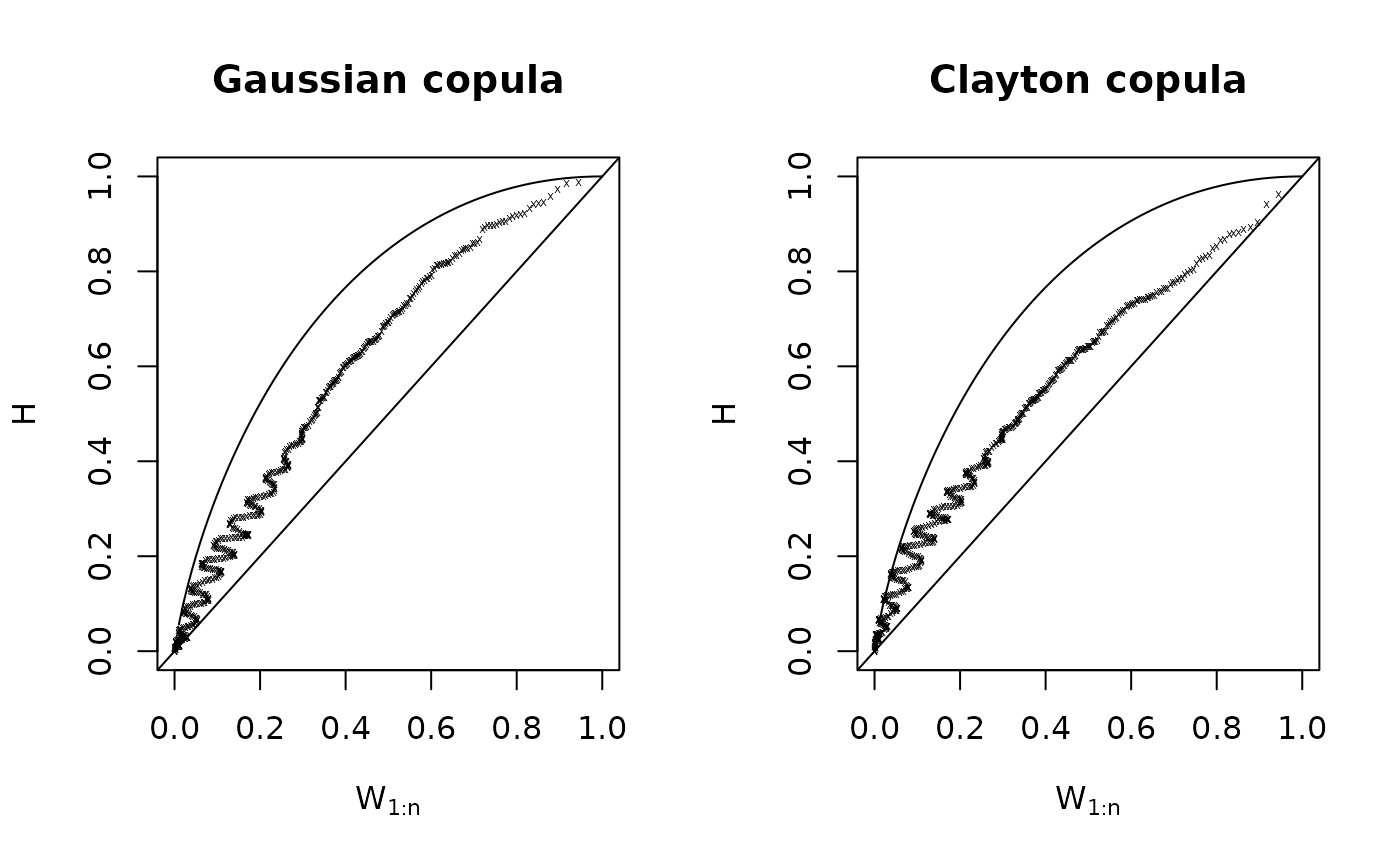
For observations $u_{i,j},\ i=1,...,N,\ j=1,2,$ the K-plot considers two quantities: First, the ordered values of the empirical bivariate distribution function $H_i:=\hat{F}_{U_1U_2}(u_{i,1},u_{i,2})$ and, second, $W_{i:N}$, which are the expected values of the order statistics from a random sample of size $N$ of the random variable $W=C(U_1,U_2)$ under the null hypothesis of independence between $U_1$ and $U_2$. $W_{i:N}$ can be calculated as follows $$ W_{i:n}= N {N-1 \choose i-1} \int\limits_{0}^1 \omega k_0(\omega) ( K_0(\omega) )^{i-1} ( 1-K_0(\omega) )^{N-i} d\omega, $$ where $$K_0(\omega) = \omega - \omega \log(\omega), $$ and $k_0(\cdot)$ is the corresponding density.

K-plots can be seen as the bivariate copula equivalent to QQ-plots. If the points of a K-plot lie approximately on the diagonal $y=x$, then $U_1$ and $U_2$ are approximately independent. Any deviation from the diagonal line points towards dependence. In case of positive dependence, the points of the K-plot should be located above the diagonal line, and vice versa for negative dependence. The larger the deviation from the diagonal, the stronger is the degree of dependency. There is a perfect positive dependence if points $\left(W_{i:N},H_i\right)$ lie on the curve $K_0(\omega)$ located above the main diagonal. If points $\left(W_{i:N},H_i\right)$ however lie on the x-axis, this indicates a perfect negative dependence between $U_1$ and $U_2$.

References

Genest, C. and A. C. Favre (2007). Everything you always wanted to know about copula modeling but were afraid to ask. Journal of Hydrologic Engineering, 12 (4), 347-368.

Author

Natalia Belgorodski, Ulf Schepsmeier

Examples


## Gaussian and Clayton copulas
n <- 500
tau <- 0.5

# simulate from Gaussian copula
fam <- 1
par <- BiCopTau2Par(fam, tau)
cop1 <- BiCop(fam, par)
set.seed(123)
dat1 <- BiCopSim(n, cop1)

# simulate from Clayton copula
fam <- 3
par <- BiCopTau2Par(fam, tau)
cop2 <- BiCop(fam, par)
set.seed(123)
dat2 <- BiCopSim(n, cop2)

# create K-plots
op <- par(mfrow = c(1, 2))
BiCopKPlot(dat1[,1], dat1[,2], main = "Gaussian copula")
BiCopKPlot(dat2[,1], dat2[,2], main = "Clayton copula")

par(op)